L’analyse par arbre de décision est une technique utilisée pour vous aider à choisir la meilleure option (ou la moins pire) lorsque vous hésitez entre plusieurs scénarios. 🤔
Dans cet article, je vais vous présenter cette technique à partir d’une question type. Si vous avez la moindre question, n’hésitez pas à commenter cet article, je vous répondrai au plus vite. Et si vous l’avez apprécié, n’hésitez pas à le partager ! 😉
ANALYSE PAR ARBRE DE DÉCISION : EXERCICE
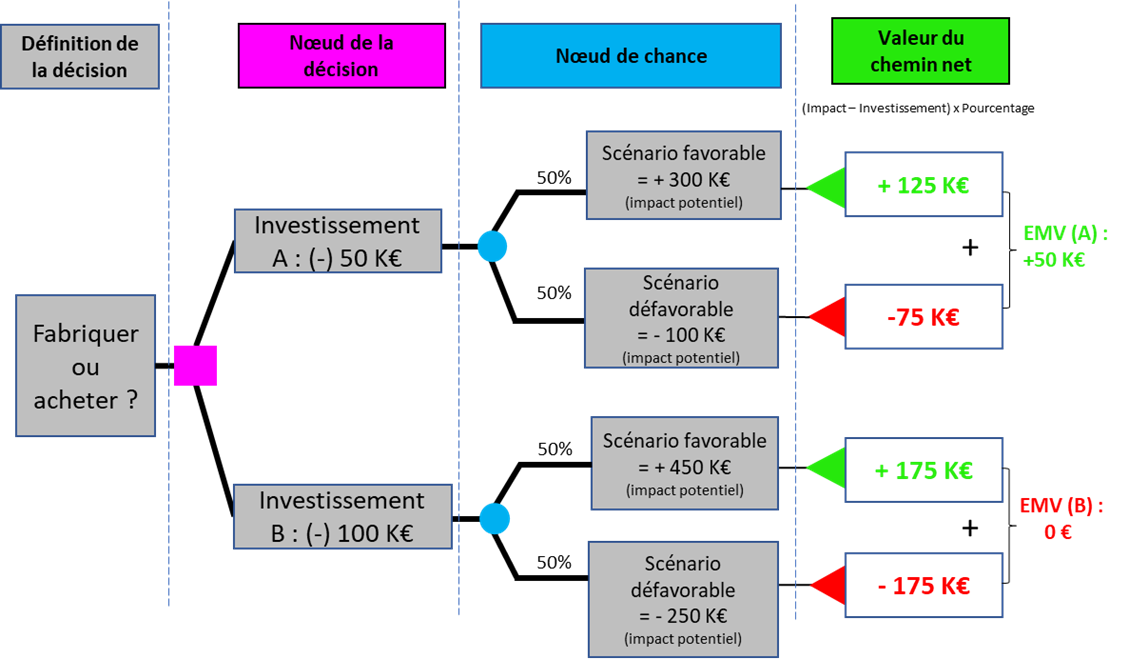
Une entreprise hésite entre fabriquer une application mobile en interne pour 50 K€ (A) ou l’acheter pour 100 K€(B). Les espérances de gain de A sont de 300 K€ si le scénario est favorable, sinon ce sera une perte de 100 K€. Les espérances de gain de B sont de 450 K€ si le scénario est favorable, sinon ce sera une perte de 250 K€. Il y a, à chaque fois, 50% de chance qu’un des 2 scénarios aboutisse.
Question n°1 : En utilisant la méthode d’analyse par arbre de décision, quelle serait le résultat de votre décision (réponse en bas de cet article) ?
- Fabriquer l’application mobile
- Acheter l’application mobile
- Vous avez besoin de faire appel à un expert
- Aucune des 2 options car une 3ème option s’impose
Question n°2 : En utilisant la méthode d’analyse par arbre de décision, quelle serait la valeur monétaire attendue (EMV : l’Expected Monetary Value) de l’investissement A (réponse en bas de cet article) ?
- 0 €
- 50 K€
- +125 K€
- -75 K€
Question n°3 : A partir de la méthode d’analyse par arbre de décision, indiquez quel est la donnée de sortie du « nœud de chance » :
- La valeur du chemin net
- La Valeur monétaire Attendue
- Le Noeud de la décision
- La décision prise
ANALYSE PAR ARBRE DE DÉCISION : CORRIGÉ
Il vaut mieux fabriquer l’application (question n°1) car l’espérance de gain (EMV) de l’investissement A (question n°2) est supérieure (50 K€) à l’espérance de gain (EMV) de l’investissement B (0 €). Enfin, (question n°3), la donnée de sortie (l’output) du nœud de chance est appelée : Expected Monetary Value (EMV).
ANALYSE PAR ARBRE DE DÉCISION : EXPLICATION
1/ Chemin de l’investissement A (Scénario favorable) : On a 50 K€ d’investissement (un investissement est une dépense donc à soustraire de l’impact en bénéfice ou perte potentiel). Soit : 300 K€ – 50 K€ = + 250 K€. Mais ce scénario n’a que 50% de chance d’aboutir. Donc on multiplie l’impact par la probabilité, donc 250 K€ * 0,5 (soit 50%) = +125 K€
2/ Chemin de l’investissement A (Scénario défavorable) : On a 50 K€ d’investissement (un investissement est une dépense donc à soustraire de l’impact en perte potentielle). Soit : -100 K€ – 50 K€ = – 150 K€. Mais ce scénario n’a que 50% de chance d’aboutir. Donc on multiplie l’impact par la probabilité, donc – 150 K€ * 0,5 = – 75 k€
Enfin, pour savoir quelle décision prendre, il suffit d’additionner les valeurs du chemin net. Soit ici pour l’investissement A : (+125) + (-75) = + 50 K€
3/ Chemin de l’investissement B (Scénario favorable) : On a 100 K€ d’investissement (un investissement est une dépense donc à soustraire de l’impact en bénéfice ou perte potentiel). Soit : 450 K€ – 100 K€ = + 350 K€. Mais ce scénario n’a que 50% de chance d’aboutir. Donc on multiplie l’impact par la probabilité, donc 350 K€ * 0,5 (soit 50%) = +175 K€
4/ Chemin de l’investissement B (Scénario défavorable) : On a 100 K€ d’investissement (un investissement est une dépense donc à soustraire de l’impact en perte potentielle). Soit : -100 K€ – 250 K€ = – 350 K€. Mais ce scénario n’a que 50% de chance d’aboutir. Donc on multiplie l’impact par la probabilité, donc – 350 K€ * 0,5 = – 175 k€
Enfin, pour savoir quelle décision prendre, il suffit d’additionner les valeurs du chemin net. Soit ici pour l’investissement B : (+175) + (-175) = 0 K€
Envie de faciliter votre chemin vers la certification PMP® ? Découvrez notre formation dédiée et notre simulateur de questions d’examen 100% francophone (avec corrigé au format vidéo). Cliquez-ici pour simplifier votre préparation et restez centré sur l’essentiel.
Un outil simple et efficace. Merci !
Merci Marlène pour ce commentaire très sympathique. Si vous avez la moindre question, n’hésitez pas à me contacter à l’adresse mail suivante : contact@prome-t.com, d’autant que maintenant vous êtes outillée ! 🙂
Ca sonne un peu plus clair pour moi, merci Tarik pour tes conseils et ton article intéressant.
Merci à toi Jackie !! Et si tu as la moindre question, n’hésite pas !!
Bravo Tarik, je ne connaissais pas ce principe, mais ce trouve cela super clair et très bien expliqué. Merci beaucoup.
Merci beaucoup Bertrand pour ce message. 🙂 Et si tu as la moindre question, tu sauras comment décider de me retrouver (Facebook, Instagram, Tik Tok, Telegram, etc.) ! 🙂
La preuve par la démonstration est vraiment utile. Merci pour la présentation de cet outil.
Merci beaucoup Freddy ! A ta disposition si tu as la moindre question, n’hésite pas !!
Dans le calcul de la valeur du chemin net, je ne comprends pas par exemple dans le scénario 1 : « Mais ce scénario n’a que 50% de chance d’aboutir. Donc on multiplie l’impact par la probabilité, donc 250 K€ * 0,5 (soit 50%) = +125 K€ « .
Ce qui a 50% de chance d’aboutir, c’est la réussite, soit un calcul de la valeur qui serait : (-50k€) + 0,5*300k€ = 100 k€
Il me semble que ce n’est pas tout le scénario qui est à multiplier par 50%, mais seulement l’occurrence de la réussite de 300k€.
Pouvez-vous m’éclairer sur la raison pour laquelle tout le scénario est *50% et pas seulement la réussite ou l’échec ?
Avec mon calcul, j’arrive sur valeur du chemin net scénario 1 : +100k€ ; scénario 2 : -100k€ ; scénario 3 : +175k€ ; scénario 4 : -225k€
Bonsoir Clem,
Merci beaucoup pour votre question. J’apprécie beaucoup votre implication.
Alors pour vous répondre, je tente un autre exemple : Imaginez que vous pariez sur un match de foot.
Vous misez 50 € sur la victoire de votre équipe. Le match se joue : 50 % de chances qu’elle gagne (vous touchez 300 €), 50 % de chances qu’elle perde (votre mise est perdue, et en plus vous devez régler 100 € de frais annexes, disons).
Il n’existe pas deux mises séparées. Il n’y a qu’une seule mise de 50 €, posée une seule fois, avant le coup d’envoi. Ce qui se joue ensuite, c’est l’issue de ce pari unique : victoire ou défaite.
Donc quand vous calculez votre espérance de gain, vous devez raisonner « par match joué », pas « par euro misé ».
Match gagné (50 % des cas) : bilan net = -50 + 300 = +250 €. Ce cas-là pèse pour la moitié de votre espérance : 50 % × 250 = +125 €.
Match perdu (50 % des cas) : bilan net = -50 – 100 = -150 €. Il pèse aussi pour la moitié : 50 % × (-150) = -75 €.
Espérance totale : +125 – 75 = +50 € — c’est le gain moyen que vous pouvez attendre par pari joué.
L’erreur à éviter : il ne faut pas lire l’arbre uniquement sur le plan mathématique, il faut le lire aussi en pensant comme un joueur (un manager, un acheteur, etc.), et non pas comme un calculateur. En regardant le tableau, on est tenté d’appliquer la formule « Impact − Investissement » ligne par ligne, comme si chaque branche était une équation indépendante à résoudre pour elle-même. Cette lecture « formule par formule » pousse à traiter la mise comme une donnée du scénario, à répéter identique dans chaque branche : -50 € dans le cas où vous gagnez, -50 € dans le cas où vous perdez.
Mais ce n’est pas comme cela qu’un match se joue. Vous ne misez pas deux fois (une fois « en cas de victoire » et une fois « en cas de défaite ») : vous misez une seule fois, avant le coup d’envoi, et c’est cette mise unique qui se retrouve ensuite prolongée par l’une ou l’autre issue. Il ne faut donc pas lire l’arbre comme « une formule par ligne », mais comme « une décision unique, suivie d’un aléa qui se scinde en deux issues possibles ». C’est pour représenter cet enchaînement — d’abord une mise fixe, ensuite un résultat incertain — qu’on partage la mise en deux moitiés, une par branche, au lieu de la recopier en entier dans chacune.